確率論 2

必要となるたびに勉強しては、すぐ忘れてしまう確率論の用語等を、自分のために一通りまとめておく。
今回参考にしたのは、以下の2冊。(両方とも値段以上の価値のある良書だと思います。)

[1]結城浩, 数学ガール(乱択アルゴリズム)
[2]平岡和幸, 堀玄プログラミングのための確率統計

複数の事象, 複数の確率変数(離散分布)

離散確率分布の場合 : 標本空間Ωにおける2個の事象 A, B を考たとき...

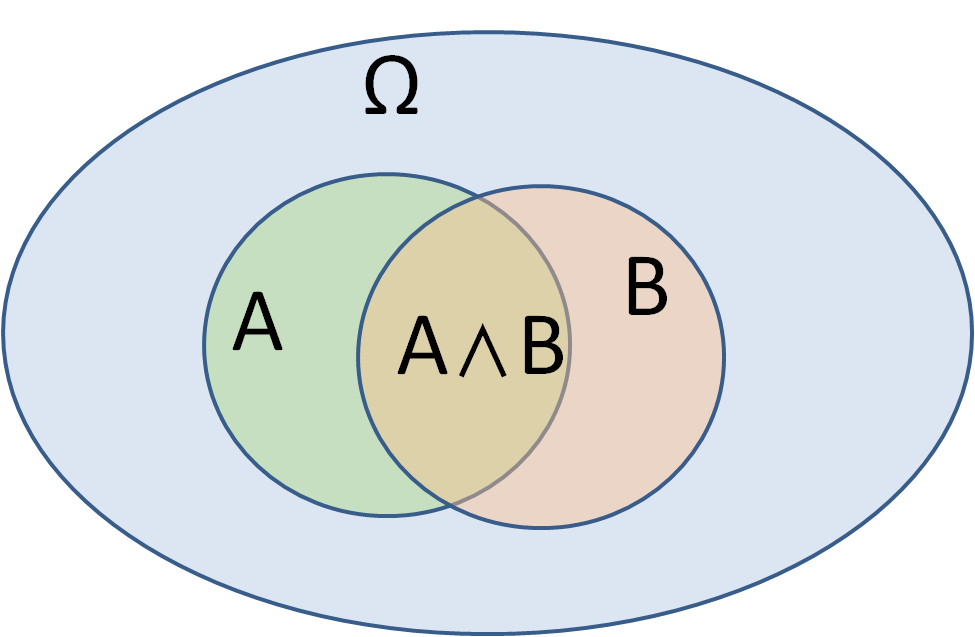
同時確率 『 P(A,B) 』: 事象A∧Bが起こる確率
周辺確率 『 P(A), P(B) 』: (事象Bはなんでもいいから)事象Aが起こる確率, と, (事象Aはなんでもいいから)事象Bが起こる確率
条件付き確率 『 P(B|A) = P(B,A)/P(A)』 : 事象Aが起こった下で事象Bが起こる確率
　　　　　　(P(A|B) = P(A,B)/P(B) , ベイズ推定においては事後確率とも呼ばれる)

例)
Ω : 日本人, 　A : 男性, 　B:血液型がO型
P(A∧B) : 日本人を一人サンプリングしたときに, その人が, 男性かつO型である確率
P(A) : 日本人を一人サンプリングしたときに, その人が, 男性である確率
P(B|A) : 日本人を一人サンプリングして, その人が男性である事を確認した下で、彼がO型である確率

確率変数の導入 : 2個の確率変数 X Yを考えて...

同時確率『 P(X=a,Y=b) 』 : X=a , Y=b となる起こる確率．　　
周辺確率『 P(X=a), P(Y=b)』: Yはどんな値をとっても良いがX=aとなる確率，と,　Xはどんな値をとっても良いがY=bとなる確率．
条件付き確率『P(Y=b|X=a)=P(X=a,Y=b)/P(X=a)』 : X=aを観測した下で，Y=bとなる確率．

例)
出る目が等確率なサイコロを2回振ったとき, 1回目のサイコロの数字をX, 2回のサイコロの和をYと，二つの確率変数XYで定義する．
P(X=4,Y=9) = 1/36 -- (4,5)のみ
P(X=4) = 6/36 -- (4,1), (4,2), (4,3), (4,4), (4,5), (4,6)の6通り
P(Y=9) = 4/36 -- (3,6), (4,5), (5,4), (6,3)の４通り
P(Y=9|X=4) = 6/36 -- X=4という事象{(4,1),...,(4,6)}のうち，{(4,5)}の1通り

同時確率と周辺確率には以下の関係がある

$\displaystyle P(X=a) = \sum_{b}^{}P(X=a, Y=b)$ X=aを固定して，Yが取り得る値全てを入れてその確率を足し合わせると、P(X=a)

$\displaystyle P(Y=b) = \sum_{a}^{}P(X=a, Y=b)$ Y=bを固定して，Xに取り得る値全てをいれてその確率を足し合わせると、P(Y=b)

同時確率分布がわかれば(すべてのXYの取り得る値の組み合わせに対して，それの起こる確率がわかれば)，XYの周辺分布や条件付き確率などが計算できる．

ベイズの公式 (離散分布)

二つのランダムに値の変わる確率変数X={a0, a1,...,an}, Y={b1,b2,...,bm}について以下が成り立つ.
　　

　
$\displaystyle P(Y=b_i|X=a) = \frac{ P(X=a|Y=b_i)P(Y=b_i) } { P(X=a) }$ $\displaystyle = \frac{ P(X=a|Y=b_i)P(Y=b_i) } { \sum_{b_i}^{}P(X=a, Y=b_i) }$ $\displaystyle = \frac{ P(X=a|Y=b_i)P(Y=b_i) } { \sum_{b_i}^{}P(X=a | Y=b_i) P(Y=b_i) }$

ベイズの公式でできる事をまとめると...

確率的に変化する『原因Y』の起こる確率が分かっており,( P(Y=b1), P(Y=b2) ,..., P(Y=bN)はknown )
任意の原因 Y=bi の下で，結果Xが X=a になる確率が分かっている, ( P(X=a|Y=b1), P(X=a|Y=b2),..., P(X=a|Y=bN) もknown)
...この下で...↓
結果 X = a が観察されたとき, その原因 Y が Y = bi である確率が分かる P(Y=bi|X=a)

例題) 関西人, 宇宙人, その他、を識別できる器械を開発した．
1) 東京の人口の
30.00%が関西人,
00.01%が宇宙人,
69.99%がその他
とする．

2) この識別器に
宇宙人を入れると， 1%の確率で関西人, 99%の確率で宇宙人, 0%の確率でその他,
関西人を入れると，95%の確率で関西人, 2%の確率で宇宙人, 3%の確率でその他,
その他を入れると， 9%の確率で関西人, 1%の確率で宇宙人, 90%の確率でその他,
と判定する.

問) 東京で一人サンプリングして識別器に入れたところ，宇宙人と判定された．この人が本当に宇宙人である確率は?

(1)が原因 Y = {関西, 宇宙, 他}の確率を表し
(2)が原因の下での結果の確率 P{X={関西, 宇宙, 他} | Y={ 関西, 宇宙, 他}}を表している事に注意．

-- 図を使った解法 --

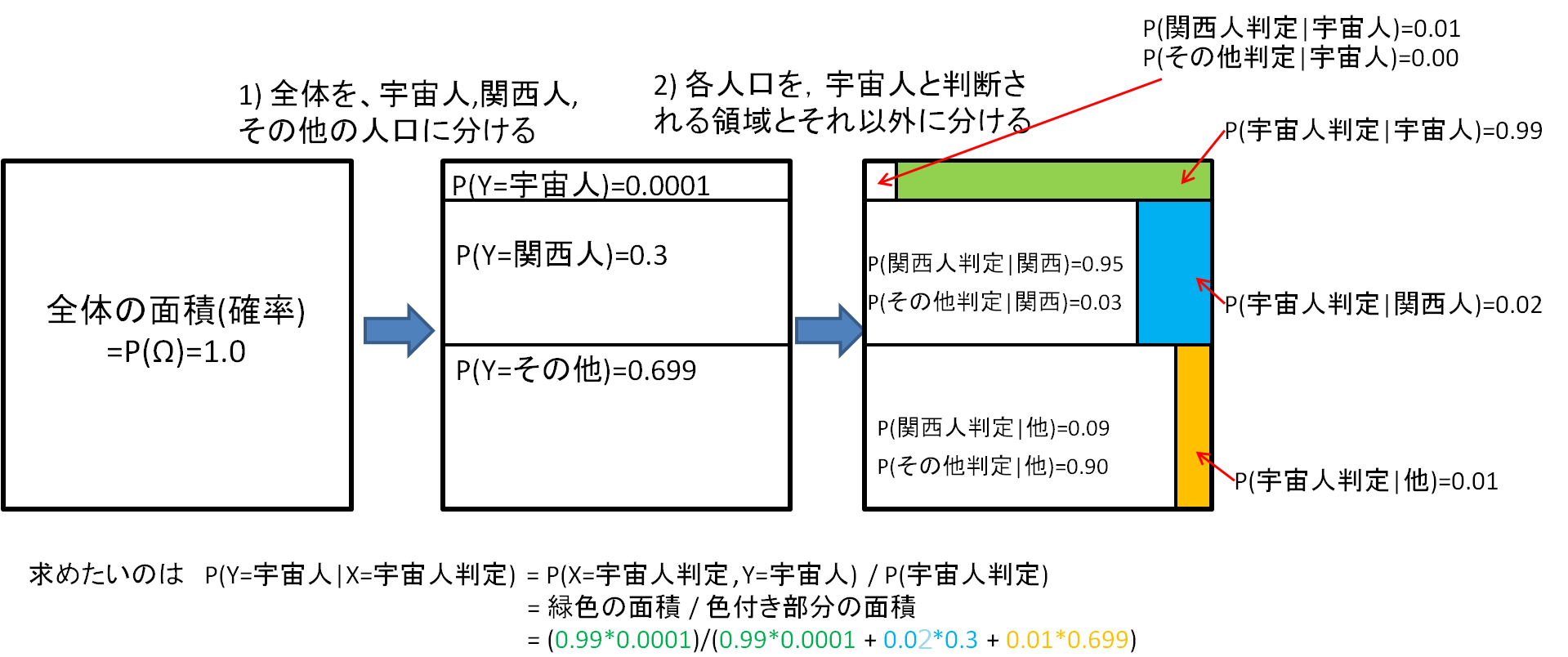
ベイズの公式を使った解法)

ベイズの公式より
P(Y=宇宙人|X=宇宙人判定)
= P(X=宇宙人判定|Y=宇宙人)P(Y=宇宙人) / P(X=宇宙人判定)
= P(X=宇宙人判定|Y=宇宙人)P(Y=宇宙人) / { P(Y=関西 , X=宇宙人判定) + P(Y=宇宙, X=宇宙人判定) + P(Y=その他, X=宇宙人判定)}
= P(X=宇宙人判定|Y=宇宙人)P(Y=宇宙人) / { P(X=宇宙人判定|Y=宇宙人)P(Y=宇宙人) +P(X=宇宙人判定|Y=関西人)P(Y=関西人) + P(X=宇宙人判定|Y=その他)P(Y=その他)}
= {0.99*0.0001}/{0.99*0.0001+ 0.02*0.3+0.01*0.6999}
=0.007558
つまりこの精度の機械で宇宙人と判断されたら，0.75%程度の確率でその人は宇宙人

　問題の前提条件(2)の一部(色つき)しか利用していない事に注意する．
　細かいことだが、ここではXYは事象として扱っており，確率変数ではない（確率変数は個々の事象を実数にマップする関数．）．
　

結局ベイズ推定は、
　　原因Yの起こる確率 + ある原因のもので結果Xが観察される確率　がわかっている下で,
　　結果X=xを観察したとき、そもそもの原因Yがyである確率を求められる P(Y=y|X=x)

複数の事象, 複数の確率変数(連続分布)

連続変数の場合，ちょうどXとYがある値になる確率，P(X=x,Y=y)，は0なので、
値が確率的に変化する2個の連続な確率変数 XとYを考える.
確率密度関数を用いて, 同時分布, 周辺分布, 条件付き分布を表す．

■ 同時分布 :
- 同時分布は同時確率密度関数 $f_{XY}(X=x, Y=y) =f_{XY}(x,y) = f_{YX}(Y=y,X=x) = f_{YX}(y,x)$ により定義される
-　同時分布が与えられれば，XとYの作る任意の集合に対して,
$\displaystyle P(a_0 \le X \le a_1,\:\: b_0 \le Y \le b_1) = \int_{a_0}^{a^1}\int_{b_0}^{b^1} \:\; f_{XY}(x,\:y) dxdy$
と確率が計算できる.(同時分布が得られたら、任意のXYの集合に対する確率分布が分かる)

-　下図は，2次元標準正規分布の同時確率密度関数

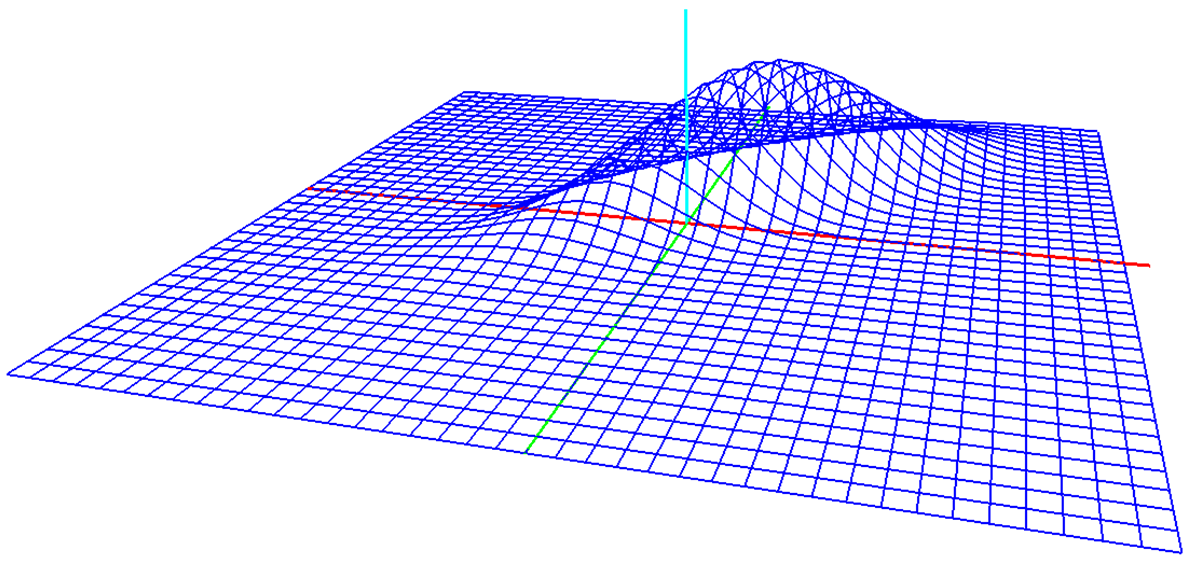
$\displaystyle f(x,y) = \frac{1}{2\pi\sigma_x\sigma_y}\sqrt{1-p^2} \exp\left{ \frac{(x-\mu_x)^2}{\sigma_x^2} + \frac{(y-\mu_y)^2}{\sigma_y^2}- \frac{ 2p(x-\mu_x)(y-\mu_y)}{\sigma_x\sigma_y}\right}$
この例では μx = 0.5, μy = 1.0, σx = σy = 1.0, p = 0.8とした.

■ 周辺分布 :
- 確率変数Xの周辺分布とは, 確率変数Yの値を気にせずに確率変数Xの確率分布を考えたもの
- 確率変数Yの周辺分布とは, 確率変数Xの値を気にせずに確率変数Yの確率分布を考えたもの
- 確率密度関数，f_X(X=x), f_Y(Y=y)で表される．
- 周辺確率密度関数は，同時確率密度関数から計算できる
$\displaystyle f_X(X=x)=\int_{-\infty}^{\infty} \:\: f_{XY}(x,\:y) dy$
$\displaystyle f_Y(Y=y)=\int_{-\infty}^{\infty} \:\: f_{XY}(x,\:y) dx$
-上式より明らかだが，次の式の形を覚えておく.
$\displaystyle P(a_0 \le X \le a_1) = \int_{a_0}^{a^1}\:\:f_X(x)dx = \int_{a_0}^{a^1}\:\:\int_{-\infty}^{\infty}\:\:f_{XY}\:\:(x,\:\:y) dydx$

■ 条件付き分布 :
- X=a₀が観察された下で, Yの条件付き確率分布は, 条件付き確率密度関数 f_Y|X(Y=y|X=a₀)を用いて表される
- Y=b₀が観察された下で, Xの条件付き確率分布は, 条件付き確率密度関数 f_X|Y(X=x|Y=b₀)を用いて表される
- 条件付き密度関数は，同時密度関数から次のとおり計算できる
$\displaystyle f_{Y|X}(y|a_0) = \frac{f_{YX}(y,\:a_0)}{ f_X(a_0) }, \;\;\;\;\;\; f_{X|Y}(x|b_0) = \frac{f_{XY}(x,\:b_0)}{ f_Y(b_0) }$

ベイズの公式 :
- 連続確率変数XYでは、ベイズの公式も同時/周辺確率密度関数を用いて表される．
$\displaystyle f_{X|Y}(a|b) = \frac{f_{XY}(a,\:b)}{ f_Y(b) } = \frac{f_{XY}(a,\:b)}{ \int_{-\infty}^{\infty} f_{XY}(x,b)dx } = \frac{f_{Y|X}(b|a)f_X(a)}{ \int_{-\infty}^{\infty} f_{Y|X}(b|x)f_X(x)dx}$

確率変数の独立性

■ 離散確率変数の場合
- 2つの確率変数X Y が, 任意の事象の組み合わせ a,bに対して次(のどれか)を満たすとき, XとYは独立であるという．
$\displaystyle P(X=a , Y=b ) = P(X=a) P(Y=b)$
$\displaystyle P(X=a | Y=b ) = P(X=a)$
$\displaystyle P(Y=b | X=a ) = P(Y=b)$

■ 連続確率変数の場合
- 2つの確率変数X Y が, 任意の事象の組み合わせ a,bに対して次(のどれか)を満たすとき, XとYは独立であるという．
$\displaystyle f_{XY}(X=a,Y=b) = f_X(X=a) f_Y(Y=b)$
$\displaystyle f_{X|Y}(X=a | Y=b ) = f_X(X=a)$
$\displaystyle f_{Y|X}(Y=b | X=a ) = f_Y(Y=b)$

確率変数XYが独立とは，XとYのあいだに関わりがないということ.　
XとYが独立なら、上記のとおり,同時分布や条件付き分布が, もう一方に依存しないものとなる．
XとYが独立なら、ベイズ推定のように， X=aを観察して Y=b の確率を推測するなどはナンセンスになる．

戻る　　確率論3へ