確率論 3
そろそろ慣れてきたので、標本空間や事象を考えず、確率変数に注目していく.
「確率変数」とは,確率的に値が変化する実数変数のことで,ある値の出やすさは確率分布によって与えられる.
「確率分布」とは, 確率1を確率変数が取りうるすべての値にどう振り分けるかを表現するもの.
戻る 確率論4へ
「確率変数」とは,確率的に値が変化する実数変数のことで,ある値の出やすさは確率分布によって与えられる.
「確率分布」とは, 確率1を確率変数が取りうるすべての値にどう振り分けるかを表現するもの.
戻る 確率論4へ
確率変数の変換
■ 離散確率変数の場合 (とても単純)
下の表の確率分布に従う離散型の確率変数Xを考える.
確率変数Xに対し, 確率変数Y Zを, Y = 2X+10, Z = X^2 と定義する.
単純に考えて,X=100の時 Y=210という値を取るから, P(X=100) = P(Y=210)=0.1が成り立つ,
X=300の時 Z=90000という値を取るから,P(X=300) = P(Z=90000)=0.2となる. この要領で表を埋めると,
確率変数は離散的な値しか取らず, 各値に対して確率が決まっているので,
単純に確率変数の値を, 変換式に代入した表を作れば良い. (離散の場合は非常に簡単)
下の表の確率分布に従う離散型の確率変数Xを考える.
| X | P(X=x) |
| 100 | 0.1 |
| 200 | 0.1 |
| 300 | 0.2 |
| 400 | 0.2 |
| 500 | 0.2 |
| 600 | 0.2 |
確率変数Xに対し, 確率変数Y Zを, Y = 2X+10, Z = X^2 と定義する.
単純に考えて,X=100の時 Y=210という値を取るから, P(X=100) = P(Y=210)=0.1が成り立つ,
X=300の時 Z=90000という値を取るから,P(X=300) = P(Z=90000)=0.2となる. この要領で表を埋めると,
| Y=2X+10 | P(Y=y) | Z=X^2 | P(Z=z) | |
| 210 | 0.1 | 10000 | 0.1 | |
| 410 | 0.1 | 40000 | 0.1 | |
| 610 | 0.2 | 90000 | 0.2 | |
| 810 | 0.2 | 160000 | 0.2 | |
| 1010 | 0.2 | 250000 | 0.2 | |
| 1210 | 0.2 | 360000 | 0.2 |
確率変数は離散的な値しか取らず, 各値に対して確率が決まっているので,
単純に確率変数の値を, 変換式に代入した表を作れば良い. (離散の場合は非常に簡単)
■ 連続確率変数の場合
Xを標準正規分布N(0,1)に従う確率変数とすると, 確率密度関数fX(x)は以下の通り.
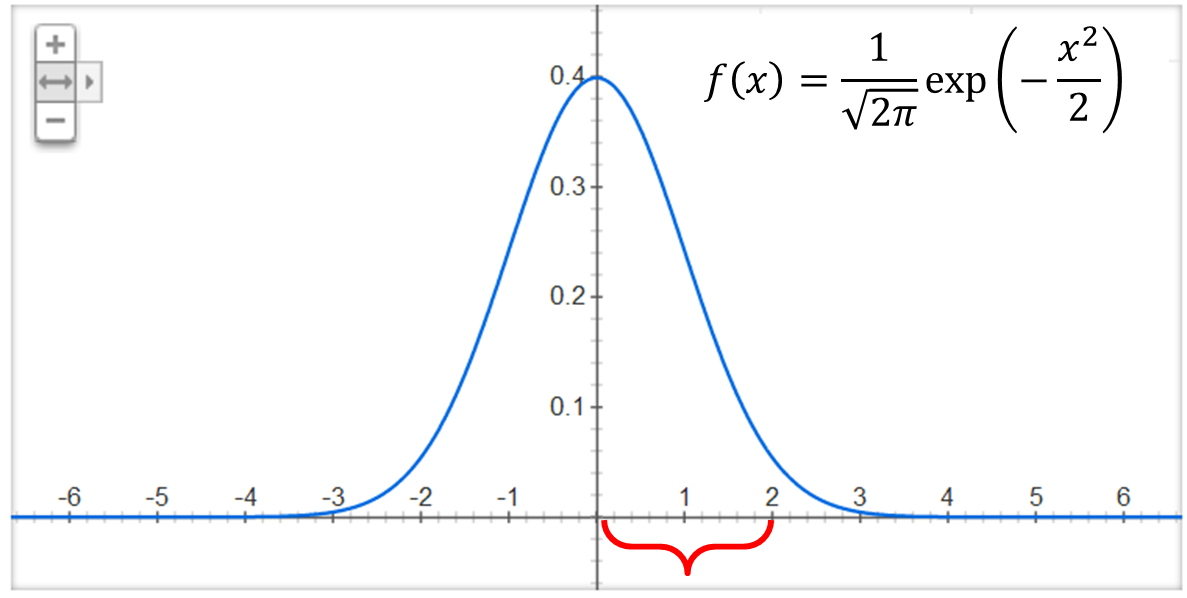
Xを標準正規分布N(0,1)に従う確率変数とすると, 確率密度関数fX(x)は以下の通り.

------------------------------
☆ここで,確率変数 Y = X + 2 の確率密度関数 fY(y) がどうなるか考える.
- 例えば , X=2 の時Y=4 ,なので, fY(4) = fX(2)
- 同様に , X=x の時Y=x+2,なので, fY(x+2) = fX(x)
- くどいけど, X=y-2の時Y=y ,なので, fY(y) = fX(y-2)
つまり,fY(y)は fx(x)を正方向に 2 平行移動したものに一致する.
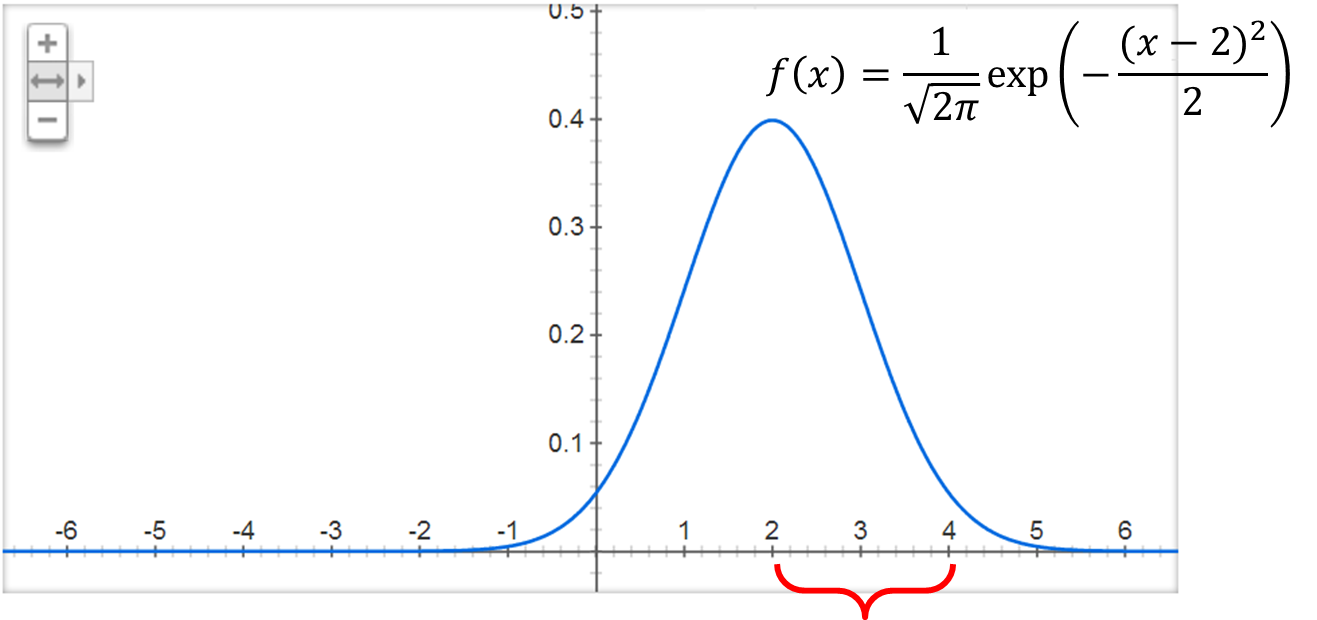
- 区間 0≦X≦2 のfX(x) の形と, 区間2≦Y≦4 のfY(y) の形が一致していることに注目.
☆ここで,確率変数 Y = X + 2 の確率密度関数 fY(y) がどうなるか考える.
- 例えば , X=2 の時Y=4 ,なので, fY(4) = fX(2)
- 同様に , X=x の時Y=x+2,なので, fY(x+2) = fX(x)
- くどいけど, X=y-2の時Y=y ,なので, fY(y) = fX(y-2)
つまり,fY(y)は fx(x)を正方向に 2 平行移動したものに一致する.

- 区間 0≦X≦2 のfX(x) の形と, 区間2≦Y≦4 のfY(y) の形が一致していることに注目.
------------------------------
☆ 次に,確率変数 Y = 3X + 2 の確率密度関数 fY(y) がどうなるか考える.
-先の例と同様すると,
- X = 2 の時 Y = 8 ,なので, fY(4) = fX(2)
- X = x の時 Y = 3x+2 ,なので, fY(3x+2) = fX(x)
- X = (y-2)/3の時 Y = y ,なので, fY(y) = fX((y-2)/3)
つまり,fY(y)は fx(x)を 横軸方向に+2平行移動して1/3倍したものに一致する
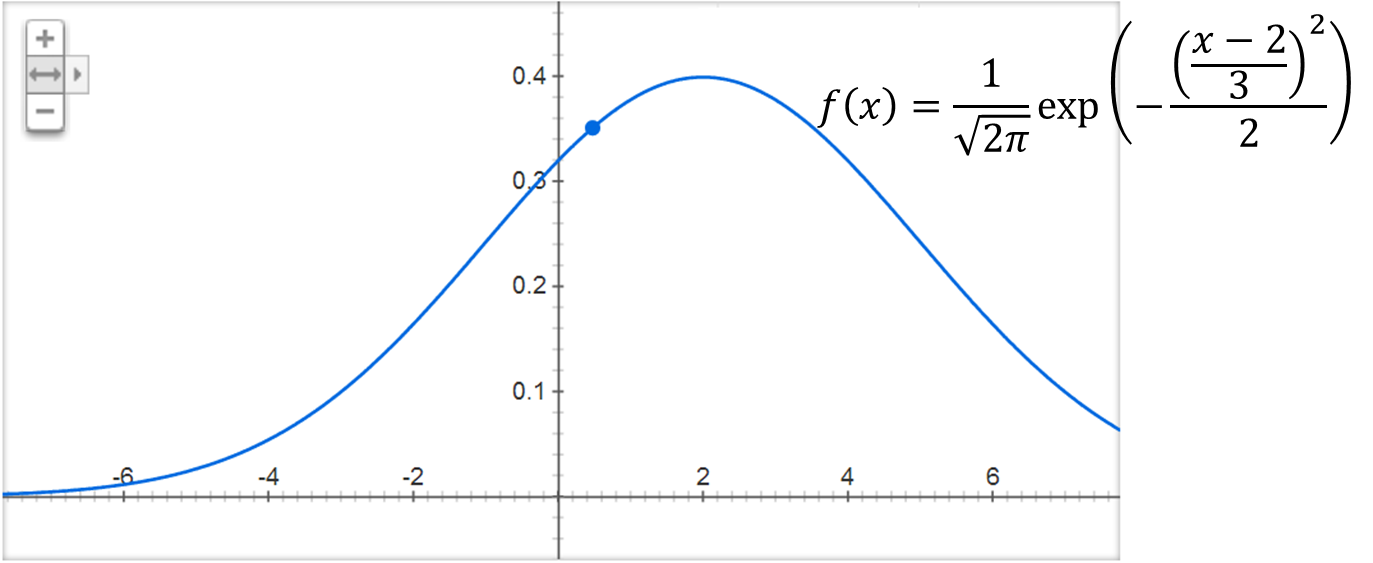
としたいところだがこれは誤り.
XとYの値の対応は良いのだが, 確率密度関数fX(x)を横軸方向に1/3倍(引き伸ばし)しているため,dx=1) を満たさなくなる.
を満たさなくなる.
☆ 次に,確率変数 Y = 3X + 2 の確率密度関数 fY(y) がどうなるか考える.
-先の例と同様すると,
- X = 2 の時 Y = 8 ,なので, fY(4) = fX(2)
- X = x の時 Y = 3x+2 ,なので, fY(3x+2) = fX(x)
- X = (y-2)/3の時 Y = y ,なので, fY(y) = fX((y-2)/3)
つまり,fY(y)は fx(x)を 横軸方向に+2平行移動して1/3倍したものに一致する

としたいところだがこれは誤り.
XとYの値の対応は良いのだが, 確率密度関数fX(x)を横軸方向に1/3倍(引き伸ばし)しているため,
全体を積分したら1になるという条件を満たすため, x方向に引き伸ばしたぶん, y方向に縮めれば良い. つまり...
- X = 2 の時 Y=8 ,なので, fY(4) = 1/3 fX(2)
- X = x の時 Y=3x+2,なので, fY(3x+2) = 1/3 fX(x)
- X = (y-2)/3 の時 Y=y ,なので, fY(y) = 1/3 fX((y-2)/3)
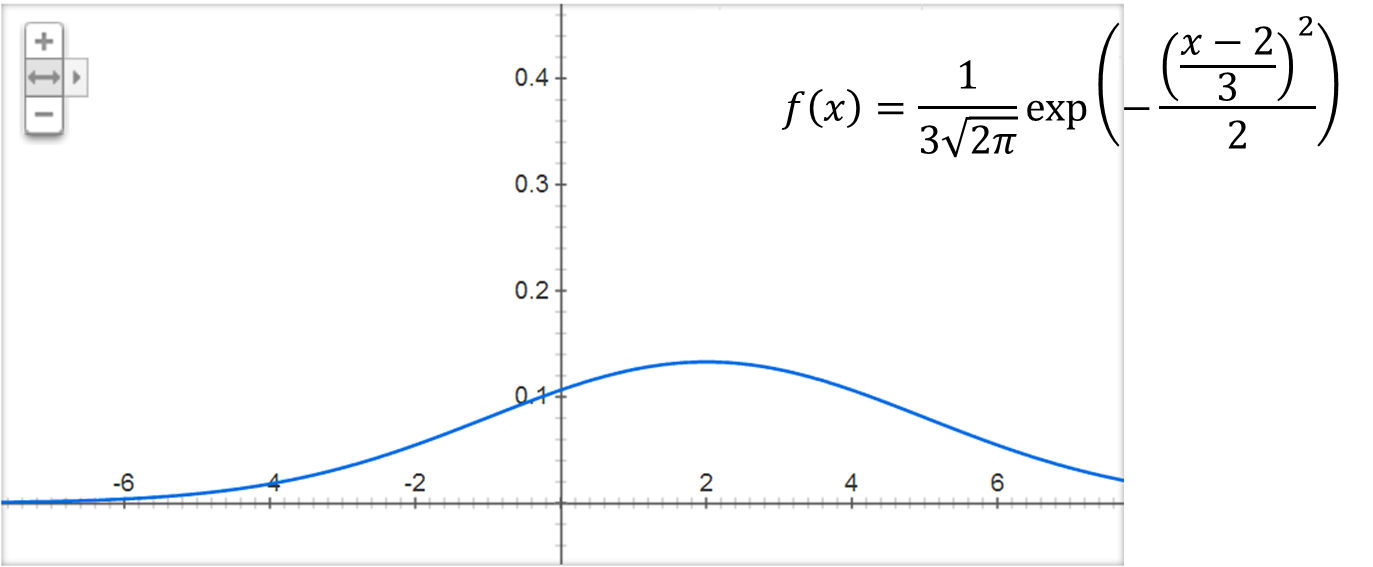
これが Y = 3X + 2の確率密度関数
- X = 2 の時 Y=8 ,なので, fY(4) = 1/3 fX(2)
- X = x の時 Y=3x+2,なので, fY(3x+2) = 1/3 fX(x)
- X = (y-2)/3 の時 Y=y ,なので, fY(y) = 1/3 fX((y-2)/3)

これが Y = 3X + 2の確率密度関数
確率変数の変換
連続確率変数Xの確率密度関数fX(x)が与えられている下で, Y = g(X)という確率変数を考える.
確率変数Yの確率密度関数は以下で与えられる
 = \left| \frac{f_X(x)}{g'(x)}\right| = \left| \frac{f_X(g^{-1}(y)}{g'(g^{-1}(y))}\right|)
ただしg(X)は, 微分可能, 逆関数g-1が存在, g'(x)≠0, 単射(a≠bならばg(a)≠g(b)) である事を仮定している.
連続確率変数Xの確率密度関数fX(x)が与えられている下で, Y = g(X)という確率変数を考える.
確率変数Yの確率密度関数は以下で与えられる
ただしg(X)は, 微分可能, 逆関数g-1が存在, g'(x)≠0, 単射(a≠bならばg(a)≠g(b)) である事を仮定している.