ドロネー三角形分割Delaunay triangulation
定義 : (一般の)三角形分割
2次元平面にN個の点群P={pi |pi ∊ R2}が与えられた時,Pの凸包の内部を,Pに属する点群を頂点とする三角形で分割した図形で,どの三角形も頂点以外にPに属する点を含まないもの.
定義 : ドロネー三角形分割
2次元平面にN個の点群P={pi |pi ∊ R2}の三角形分割の内,任意の三角形の外接円の内部にPに属する点を含まないもの.4点以上の点が同一円周上る場合,ある三角形の外接円上に,三角形を構成する頂点以外のPに属する点が乗る場合がある[1].
制約なしドロネー分割---(逐次加点法)
既にドロネー三角形分割がなされている図形を仮定し,それに新たな点を追加する.この時,追加する点を含む三角形を分割し,ドロネー三角形分割の性質が保たれるようにEdge Flipを繰り返す.
A1) 点群を包含する十分大きな三角形(super triangle)を追加する
A2) i番目の頂点piを三角形分割図形に追加
A2-1) piを含む三角形ABCを発見し, この三角形をAB pi, BC pi, CA pi の3個の三角形に分割.
この時, 辺AB, BC, CAをスタックSに積む (最初の一点のときには,super triangleが見つかる).
A2-2) スタックSが空になるまで以下を繰り返す
A2-2-1) スタックSの一番上のedgeをpopする.これを辺ABとする
A2-2-2) 辺ABを含む2個の三角形をABCとABDとする
if(三角形ABCの外接円内にDが入 る) 辺ABをflipし,辺AD/DB/BC/CAをスタックSにpushする
else 何もしない
A3)super triangleとそれに関する頂点を破棄する.
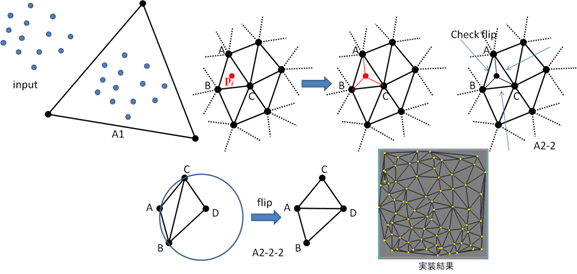
図1
このアルゴリズムの重要な点は,新たな点を追加し,その点を含む三角形を分割した後に,すべての三角形がドロネー性を満たすようにEdge flipを繰り返す点.この逐次的なEdge flipを効率的に計算するには,方向を持つHalf Edgeデータ構造を使うとよい.A2-2-2では,edge flip後4辺をスタックに追加しているが,Half edgeを用いると,今まで検索してきた方向を考慮し,2辺のみをスタックに積めば良い.
制約つきドロネー分割---(逐次加点法)
制約付きドロネー分割では,入力点群P={pi |pi ∊ R2, i= 0,1,...n-1}に加え,制約線分群E{ (i, j) |i ,j∊{0,1,...,n-1}}が与えられ,制約線分を跨がない範囲でドロネー性を満たす必要がある.(雑に言うと,制約線分の要素がedgeになるように,かつ,なるべく,ドロネー性が満たされる必要がある.詳しくは[1]).加点法[2,3]で実装する場合,制約なしとの大きな違いは次の2点,
+1) edge flipの条件 :ドロネー性より制約線分が満たされているかどうかを優先する
+2)制約線分が満たされてない場合の事後処理 : Edge flip条件を変更するだけでは,制約線分が満たされない場合があるので後処理で,制約線分の復帰をする必要がある.
お茶大, 伊藤先生ら[3]により,まず制約に関する頂点を追加し,次に制約に関係ない頂点の追加を行うと高速に計算できる事が紹介されているので,以下でもそれを用いる.
B1) 点群を包含する十分大きな三角形(super triangle)を追加する
B2) 線分制約にかかわる頂点piを図形に追加
B2-2) piを含む三角形ABCを発見し, この三角形をAB pi, BC pi, CA pi の3個の三角形に分割.
この時, 辺AB, BC, CAをスタックSに積む.
B2-3) スタックSが空になるまで以下を繰り返す
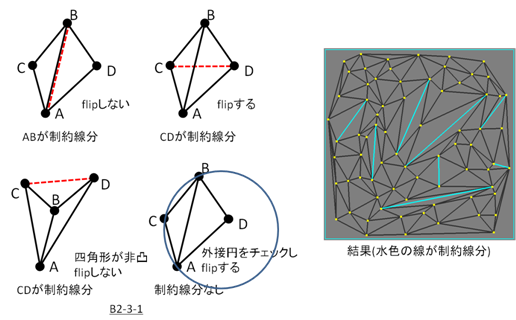
B2-3-1)スタックSから辺をpopし,これを辺ABとする.
辺ABを含む2個の三角形をABCとABDとする
if( ABが線分制約である ) 何もしない
else if( CDが線分制約であり四角形ABCDが凸) 辺ABをclip,辺AD/DB/BC/CAをスタックに積む
else if( ABCの外接円内にDが入る ) 辺ABをflip,辺AD/DB/BC/CAをスタックに積む
else 何もしない
B3) 制約線部の復帰を行う
B3-1)各制約線分ABについて以下を繰り返す
B3-2)現在図形とABと交差する全てのエッジをキューKに挿入
B3-3)キューKが空になるまで次を繰り返す
B3-3-1)キューKの先頭要素をpopし辺CDとす.CDを含む2個の三角形をCDE, CDFとする
if( 四角形ECFDが凸 ) エッジCDをflip. 新たなエッジEFをスタックNにpush.
else エッジCDをキューKに後ろからpush.
B3-3) B-2-3と同様の処理をキューNに対して行う(新たなエッジのドロネー性の確認を行う)
B3) 線分制約にかかわらない頂点piの追加
B3-2) piを含む三角形ABCを発見し, この三角形をAB pi, BC pi, CA pi の3個の三角形に分割.
辺AB, BC, CAをスタックSに積む.
B3-3) スタックSについてB2-3-1と同様の処理を繰り返す
B4) super triangle頂点とそれに関わる全てのエッジを取り除く
上記アルゴリズムも,Half Edgeデータ構造を利用する事で効率化する事が可能.また,B2-3-1のedge flip時にそのedgeを囲む四角形の凸チェックをする必要がある.参考文献[3]では,上記アルゴリズムより複雑な事をしている.[3]では,制約線分に関する頂点を一点追加した後,すべての制約線分と生成図形との間で交差判定を行う.もし,一本の制約線分と2辺で交差する三角形が発見された場合,その頂点の追加作業を巻き戻し,その頂点を後回しにする.この方法の利点は,交差判定の回数が減らせ,計算効率が高い点である.ただし,このアルゴリズムを実装してみた結果,複雑な線分制約を与えた場合,どの頂点を追加しても,制約線分と2辺で交差する三角形が生成されてしまうような,手詰まり状態になる事があった.この場合は, Sloanら[2]制約線分復帰操作(B2)をする必要があった.(複雑な制約線分では手詰まりが避けられないと思うが,”必ず手詰まりになる”や”手詰まりにならない頂点列順が存在する”などの証明は今のところ発見できていない。)
[1] 杉原 厚吉, グラフィックスの数理 (情報数学講座 (13)), 共立出版, 1995.
[2] Sloan, S. W., A Fast Algorithm for Generating Constrained Delaunay Triangulations, Computers and Structures, 47, 3, 441-450, 1993.
[3]伊藤貴之, 山田敦, 井上恵介, 古畑智武, 嶋田憲司, 制約つきDelaunay三角メッシュ生成法の効率的な実装方法, 全国大会講演論文集 第55回平成9年後期(4), 252-253, 1997-09-24
井尻敬 @ 生物情報基盤, 理研
2011/12/26