微分幾何学1

戻る topへ

 

概要: パラメータ表示された曲線と曲面の曲率の導出をまとめておく．

 

1平面曲線の表現方法

　平面曲線には3種類の表現方法がある．右は半径rの円の例．

- Explicit  (陽的表現)       :    　:  

- Implicit  (陰的表現)       :  　:  

- Parametric(パラメータ表示) : 　　:　

ここではパラメータ表記に注目する．

 

 

1-1平面曲線の弧長パラメータ表記

 

　あるパラメータt により表現された，2次元曲線C上の点p(t)を考える．ただし，パラメータtが増加するとき，p(t)は常に同じ方向に進むものとする．

C:  …(1)

p(t)をtで微分すると，tを時間と考えた時の，曲線の速度ベクトルが得られる．時間での微分であるためニュートンのドットを用いて，，と書かれる事が多い．

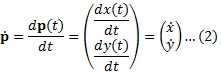
端点O(t=0)から点P(t=t)の距離(弧長)は，速度ベクトルの大きさの時間積分で得られる．

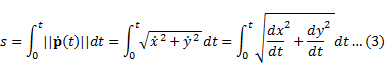
ここで，式(3)には，点Pの位置を表すtとpのパラメータとしてのtが入っており，ややこしいので， = と書いても良い．式(3)は定性的には，弧長sはtの関数であるという意味(当たり前)なので，

と書ける．パラメータtが増加するときp(t)は止まることなく常に同じ方向に進むので，f(t)は単調増加関数になる．つまり，fには逆関数f^-1が存在する．

このtを式(1)に代入すると，曲線C上の点pをその弧長sをパラメータとして表現できる．

これを曲線の弧長パラメータ表現と呼ぶ．ただし，は，存在が明らかでも，f^--1を綺麗な形で書く事が困難な場合が多く，実際の計算にはほとんど必要ない(教科書中では必要とされているのをあまり見ない)．

  弧長パラメータsで表される曲線pの速度ベクトルp'の長さを考える．('は，パラメータsでの微分を表す．)

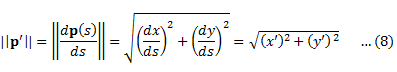
弧長パラメータsによる微分は，’を用いて表現されることが多い．ここで式(3)の両辺をで微分すると，下記の通り孤長パラメータsと時間パラメータtの関係式が得られる．

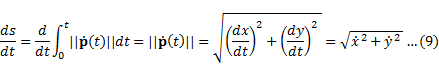
ここで，式(8)は式(9)用いると，以下の通り計算できる．

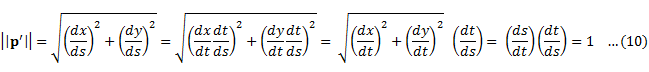
つまり，孤長パラメータであらわされた平面曲線の速度ベクトルの長さは1になる．また，曲線C上の点(s=s⁰)において，曲線Cの式をテイラー展開し2次以上の項を無視すると，

この式は，点s=s0で曲線Cの一次近似，すなわち接線を表す．つまり．p'は接線方向のベクトルを表す．

 

 

 

1-2平面曲線の曲率

 

　平面曲線上の点p(t)における単位接線ベクトルをe₁と定義し，これを90度反時計周りに回転したベクトルをe₂とすると，p(t)における局所座標系が定義できる．

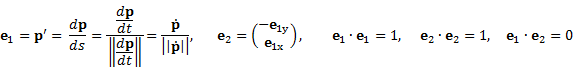
ただし，sは弧長パラメータである．曲線上を微小距離進んだ時の接線ベクトルe₁の変化割合を，曲線の曲率ベクトルkと定義する．

e₁・e₁=1の両辺を微分すると，e₁・e'₁=0より，e₁とe'₁は直行する．つまり，e'₁はe₂のスカラー倍(k)で表せる．

この係数kを曲率と呼ぶ．kがe₂方向を向いているときに正になる．

 

　ざっくりまとめると，曲線pを弧長パラメータsであらわした時, p(s)の1階微分が接線p'=e₁に，2階微分が曲率ベクトp''=kになりその大きさk=||p''||が曲率になる．曲率の正負は，接線ベクトルe₁= p'を90度回転したベクトルe₂と曲率ベクトルkとが同じ方向を向く時，正となる．また，曲率ベクトルとe₂は平行になる．

 

練習． 平面曲線p(t) = (x(t), y(t))の曲率を求めよ．ただし，tは任意のパラメータとする． 

以下，ドットはtでの微分を表す．

まず，p(t)を弧長パラメータsで表した時のsとtの関係式は以下である．

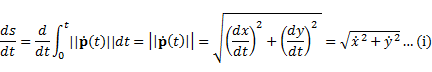
平面曲線の曲率は弧長パラメータの二階微分の絶対値なので，(i)に注意して式変形を施すと，

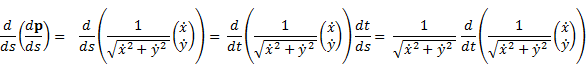
よって

また，tが弧長パラメータなら，(x'x'+y'y')=1の下で，上記と同様の計算を行い

となる．

 

 

 

1-3空間曲線

 

　パラメータtにより表記される三次元空間曲線を考える．

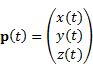
平面曲線のときと同様に，弧長sを求める事が出来，

この弧長パラメータで，曲線を再定義する事が出来る．

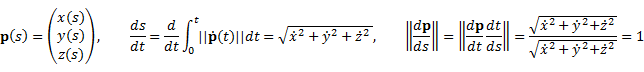
この曲線の接線ベクトルe₁と加速度ベクトルe'₁は，それぞれ1階微分，2階微分により，以下の通り求まる． 

弧長パラメータsを用いると接線ベクトルの長さ|||が自然に1になる．また，加速度ベクトルの大きさを曲率kと定義する．また，e₁・e₁=1の両辺を微分するとe₁・e'₁=0なので，e₁とe'₁は直行する．上記のe₁, e'₁, kを用いると曲線p上に正規直行座標系が定義できる．

このe₁, e₂, e₃をそれぞれ，接線，主法線，従法線と呼ぶ．

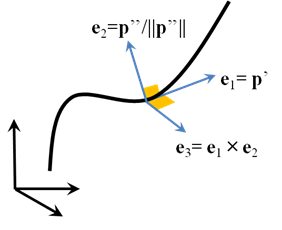
　曲線関係で重要な事を以下にまとめておく．

-任意のパラメータtで表現された曲線pを，弧長sをパラメータとして表現できる．(tが増加するときp(t)が停留することなく同一方向に進む必要はある)

-弧長パラメータsを用いると，接線の長さ||p'||=1となる．また，という関係式が必要になる事が多い

-曲率は，弧長パラメータ表現した下での，加速度ベクトルの長さで定義される．

-曲線上の点に，正規直行座標系e₁, e₂, e₃を定義する事が出来，その方向を，接線，主法線，従法線と呼ぶ．

 

 

 

曲面の曲率

 

曲面は，2個のパラメータにより表現される位置ベクトルp(u, v)の動く軌跡として表現される．

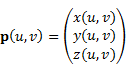
このパラメータuとv一方の変数を固定し，もう一方を動かすと，曲面に乗る2本の曲線が描かれる．

また，この曲線の接線ベクトル(速度ベクトル)は以下で表せる。

ここでは，p_u，p_vが一次独立である場合を考える．曲面の任意の接ベクトルはp_u，p_vにより張られるので，ap_u+bp_vと書く事が出来る．このベクトルの長さの二乗は，

これを曲面の第一基本形式と呼ぶ．第一基本形式は全微分dp=p_udu + p_vdv を用いて，

Ⅰ = dp・dp = Edudu+ 2 Fdudv+Gdvdv

とも書ける．これは，曲面pの微小接ベクトル(dp = p_udu+ p_vdv)の長さの二乗を表す．全微分(dp=p_udu + p_vdv)とは，多変数関数の全ての変数が微小量動いた時の全体の変化量である．duやdv微小変化量を表す変数と考えておけば良い．

 

  u-v空間中に曲線C: (u(s), v(s))があるとき，この曲線は，曲面p上でも曲線C_pを描く.

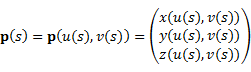
パラメータsは，曲線p(s)の弧長になるように定められているとする．

この曲線のuv平面での接ベクトルは，(du/ds, dv/ds)であり,三次元空間での接ベクトルは，以下の通りである． (二変数関数のチェーン規則を適用した)

さらに，この曲線の曲率kはp(s)の二階微分の長さであり，この曲線の法線ベクトルe₂はp(s)の二階微分を正規化したものなので，以下の通りとなる，

一般に，上式の表す曲線p(s)の法線ke₂と，曲面p(u,v)の法線nは平行で無い事に注意．今，曲面p(u,v)の法線nは，2本の接線ベクトルを用いて以下のように書ける．

ここで，曲面上を動く曲線p(s)の二階微分(ke₂)を，曲面p(u,v)の法線nに射影した量を考える．

これを曲線pの法曲率と呼び，この式の形を第二基本形式と呼ぶ．ただし，L=p_uu・n, M=p_uv・n, N=p_vv・nは第二基本形式の係数である．式(15)は曲線p(s)の曲率ベクトルを表し，曲面p(u,v)の法線とは無関係なのに対して，式(16)の法曲率は，曲線曲率の曲面に依存する成分を取りだしたものである．

 

ややこしいので噛み砕く．

1)三次元空間に曲面 p(u,v)がある．

2)uv空間の平面曲線C: (u(s), v(s))は，曲面上でも曲線C_p:( p(u(s),v(s)) )を描く (パラメータsをC_pの弧長になるようにとる)

3)曲線Cの接線は，(du/ds, dv/ds)

4)曲線C_pの接線はp_u du/ds + p_v dv/ds (p_u p_vが作る行列をpのヤコビヤンと考えても，2変数チェーンルールを使ったと考えてもOK)

5)曲線C_pの曲率は式15

6)曲線C_pの法曲率は式16

7)式16をよく見ると，法曲率は，曲面から得られる量(L=p_uu・n, M=p_uv・n, N=p_vv・n)だけでなく，接線方向を表す量(du/ds, dv/ds)に依存する．(このu(s),v(s)は，|| p_u du/ds + p_v dv/ds ||=1を満たすようになっている必要がある．)

 

 

  今，曲面p(u,v)上のある点Pにおける任意の接ベクトルは，u方向v方向への微小変化量abを用いて，p_ua+p_vbとかける．この接ベクトルの長さをAとすると，正規化した接ベクトルはp_ua/A+p_vb/Aであり,式16から，点Pにおける法曲率は，

となる．ここで(du, dv)を色々と変化させた時の法曲率の最大最小値をそれぞれk₁k₂とし，(k₁+k₂)/2を平均曲率，k₁k₂をガウス曲率と呼ぶ．上式の極値を求めるため，∂k/∂a=0, ∂k/∂b=0計算したいが，複雑すぎてうまくいかない．そのため，式(17)を次のように変形し，

両辺を, abで偏微分して∂k/∂a=0, ∂k/∂b=0と置く．

この式を満たす(a,b)!=(0,0)が法曲率の最大最小値を与える方向ベクトルで，この式を満たすkがそのa, bに対する法曲率の極値になる．ここで，(a, b)!=(0,0)となるa,bのペアが存在するためには，上の連立方程式が解をもってはいけないので，行列式がゼロ，つまり，

が満たされる必要がある．さらに，上式はkの二次式なので2個のk₁k₂が解となり，

が得られる．この時，最大値を最小値をとし，それを与える(a₁, b₁)，(a₂, b₂)をを主方向と呼ぶ．以上より，ガウス曲率と平均曲率が，第一，第二基本形式の係数のみで求まる事がわかった．

 

今後の予定

+曲面上の幾何とラプラスベルトラミオペレータ

+陰関数表現における曲率

 

井尻敬 @ 生物情報基盤, 理研 

勉強した日 2011/2/10