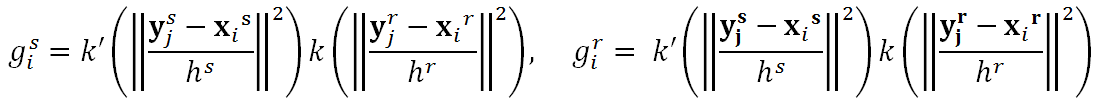Mean Shift Clustering

Mean Shift Clustering
　　　　　　　　　　
戻る topへ
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　戻る

概要: Mean Shift法[1]とは，d次元空間内に点群xiが分布しているとき，その密度の極大点(node)を発見する手法である.
より厳密には、点群x_iを標本点として出力し得る”確率密度関数”の極大点を発見する手法である．

計算は最急降下法の原理を用いる．
　1. 空間内の任意の点を初期位置とし，
　2. 徐々に密度(確率密度)の大きな方へ向かって移動して，
　3. 極大点(node)に到達すると計算を止める．

点群のクラスタリングや画像の特徴保存フィルタとして応用できる．

[1] Dorin Comaniciu , Peter Meer , Senior Member, Mean shift: A robust approach toward feature space analysis, IEEE Trans. on PAMI, 2002.

カーネル密度推定 Kernel density estimation (準備)

　　d次元空間にばらまかれたN個の点，x₁, x₂, ..., x_N ∈R^d，を考える．
　　この点群をある確率分布に従う標本と考えた時，任意の点x∈R^d における確率密度関数f(x)以下の通りである．

　　　　 $\displaystyle f(\bf{x}) = \frac{c_{kd}}{Nh^d}\sum_{i=1}^{N}k\left( ||\frac{\bf{x}-\bf{x}_i}{h}||^2 \right)$ ...(1)
　　
　　k(t)は，カーネル関数であり，色々な関数が利用される．

　　Gaussian カーネル　　　 $\displaystyle k(t) = exp \left( -\frac{||\bf{x}||^2}{2} \right)$
　　
　　Rectangular カーネル　 $\displaystyle k(t) = 1 \;\;\;\;\;\;\;\;\;\; (|t|<1), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\; (other)$ 　

　　Epanechnikovカーネル $\displaystyle k(t) = 1-t \;\;\;\;\;\;\;\;\;\; (|t|<1), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; 0 \;\;\;\;\;\;\;\;\;\; (other)$

　　c_kdは，K(x) = c_kdk(||x||²) というK(x)の全体の積分を1にするための，正規化係数．(最終的な計算には使わない)
　　　　　 $\displaystyle c_{kd} = \int_{\Omega} k( ||\bf{x}||^2 )d\bf{x}$

上の式の説明 :
d次元空間にばらまかれたN個の点，x₁, x₂, ..., x_N ∈R^d，がを考える．
この点群をある確率分布に従う標本と考えた時，任意の点x∈R^d における確率密度関数f(x)は，
Kernel density estimation法により以下のように推定できる．
　　　 $\displaystyle f(\bf{x}) = \frac{1}{N}\sum_{i=1}^{N}K_H( \bf{x}-\bf{x}_i)$
　　　 $\displaystyle K_H(\bf{x}) = ||H||^{-1/2} K(H^{-1/2}\bf{x})$

ここで，H∈R^d×dはバンド幅行列で，K(x)は，有界(値域が有限)､Compact support、正規(定義域全体での積分が1)、対称、指数関数減衰の条件を満たすカーネルである．

実用的には，バンド幅行列H=diag(h²,h²,...h²)とする事が多い．h∈Rはバンド幅パラメータ．
すると、点xの確率密度関数f(x)は，以下の通り．
　　　 $\displaystyle f(\bf{x}) = \frac{1}{N h^d}\sum_{i=1}^{N}K\left( \frac{\bf{x}-\bf{x}_i}{h} \right)$

さらに，ベクトル値を引数に取るカーネルK(x)は，スカラー値を引数に取るk(t)を用いて次のように表す事が多い．
　　　 $\displaystyle K(\bf{x}) = c_{kd} k(||\bf{x}||^2)$
　　

こうすると，自然にK(x)の放射対称性が満たされる．c_kdは，K(x)の正規性を満たすための係数である．
以上より，上の式(1)を得る．

カーネル密度関数f(x)の微分(準備2)

　　式(1)の勾配は以下の通りである．
　　　 $\displaystyle \nabla f(\bf{x}) = \frac{2c_{kd}}{Nh^{d+2}} \sum_{i=1}^{N}k'\left( ||\frac{\bf{x}-\bf{x}_i}{h}||^2 \right) (\bf{x}-\bf{x}_i)$

　　これは以下の通り変形できる．
　　　 $\displaystyle \nabla f(\bf{x}) = \frac{2c_{kd}}{Nh^{d+2}} \sum_{i=1}^{N} ( g_i \bf{x}_i - g_i \bf{x})$ 　　　　ただし， $\displaystyle g(t) = -k'(t),\;\;\;\;\;\;\;\;\; g_i = g\left( ||\frac{\bf{x}-\bf{x}_i}{h}||^2 \right)$ 　と置いた．(k'はkをtで偏微分)

　　さらに，
　　　 $\nabla f(\bf{x}) = \frac{2c_{kd}}{Nh^{d+2}} \left{\sum_{i=1}^{N} g_i \right} \left{ \frac{ \sum_{i=1}^{N}g_i\bf{x}_i }{ \sum_{i=1}^{N}g_i } - \bf{x} \right}$ 　　　　　...(2)
　　この形が後々重要.
　　式変形の過程で，Σgi>0 を仮定した.これは前述のGaussianカーネルとかEpanechnikovカーネルを使っていれば満たされる.

　　
　　特に説明することもないけど，よく利用される以下の公式を使った．ボールドxは，d次元ベクトル．

　　 $\nabla ||\bf{x}|| = \frac{\bf{x}}{||\bf{x}||}$
　　

Mean Shift Procedure

　　d次元空間R^dにばらまかれたN個の点，x₁, x₂, ..., x_N ∈R^d，と，任意の点y∈R^dについて，
　　点y付近の点群密度の極大点(node)は，次の通り求められる．

　　1. 初期化 y₀ ← y
　　2. 更新(Mean Shift) $\bf{y}_{t+1} \leftarrow \frac{ \sum_{i=1}^{N} g_i \bf{x}_i}{ \sum_{i=1}^{N} g_i}$ 　　ただし　 $\displaystyle g(t) = -k'(t),\;\;\;\;\;\;\;\;\; g_i = g\left( ||\frac{\bf{y}_t-\bf{x}_i}{h}||^2 \right)$
　　3. ||y_i+1-y_i|| < threshold　となるまで2.を繰り返す
　　
　　4. 収束したらその y_iを出力

　　
説明．

式(2)は非常に重要な形をしている．
まず、前半 $\frac{2c_{kd}}{Nh^{d+2}} \left{\sum_{i=1}^{N} g_i \right}$ は，GaussianカーネルやEpanechnikovカーネルを用いた場合，正になる．

後半　 $\left{ \frac{ \sum_{i=1}^{N}g_i\bf{x}_i }{ \sum_{i=1}^{N}g_i } - \bf{y}_t \right}$ 　は，Mean Shiftと呼ばれる項で，点xの近傍のデータ点群の加重平均位置とx自身の差分ベクトルである．
a1) このMean Shiftベクトルが，▽f(y_t)の方向を表す．
a2) このMean Shiftベクトルは，方向だけでなく、長さも内包している．つまり，極大点から遠い点ではMean Shiftベクトルは大きくなり，
　　計算が進み，y_tが極大点に近づいてくると，Mean Shiftベクトルは徐々に小さくなる．

　　最急降下法を使えば，次の通りyiを更新できる．
　　 $\bf{y}_{t+1} \leftarrow \bf{y}_{t} + h \nabla f( \bf{y}_{t})$ 　　

　　ただし、hはタイムステップ．ここで(a1)を踏まえると，
　　 $\bf{y}_{t+1} \leftarrow \bf{y}_{t} + h \left( \frac{ \sum_{i=1}^{N} g_i \bf{x}_i}{ \sum_{i=1}^{N} g_i} - \bf{y}_t\right)$

　　となる．さらに(a2)の長さを内包していることに注目すると h = 1として良い(一番問題になるオーバーシュートが起きない)ので、
　　 $\bf{y}_{t+1} \leftarrow \bf{y}_t + \left( \frac{ \sum_{i=1}^{N} g_i \bf{x}_i}{ \sum_{i=1}^{N} g_i} - \bf{y}_t\right)$
　　
　上のアルゴリズム中のMean Shiftの更新と同じものが得られた．　

Mean Shift Clustering
　　Mean Shift Procedure algorithmはクラスタリングにおうよう出来る．
　　
　　d次元空間R^dにばらまかれたN個の点，x₁, x₂, ..., x_N ∈R^d，が入力された下で．
　　密に分布する点群をクラスタとして分割する．

　　1. 各点x_i にMean Shift Proceduerを適用し，収束位置x_i^c を計算する
　　2. 任意の2個の点　x_i　x_k　について，その収束位置が閾値以下なら，(　||x_i^c - x_k^c|| < thresh　)この二点を同じクラスタに入れる．

　これにより，同じ密度の極大点(node)に属する点群が同じクラスタになるよう，分割できる．

　　

　　上の手法は，入力点群全てに対してMean Shiftを計算するので，計算コストが高い．
　　計算コスト削減のための，下のような手法もある．　

　　1. d次元空間のデータ点群の分布する全体を覆う十分密な初期点群 y_i を用意する．
　　2. y_i 全てにMean Shift Procedureを適用し収束点 y_i^cを計算する．
　　3. 十分近い収束点を持つy_iに同じラベルを付加する．
　　4. y_iは空間全体を覆う点群なので，すべてのy_iのMean shift procedure計算時に少なくとも1つのカーネルがx_iを訪れている．
　　　　x_iに，x_iを訪れたカーネルのラベルを付加する．
　　　　異なるnodeへ収束する複数カーネルがx_iを訪れた時は，多数決でラベルを決定する．

　（でも，xiより少ない数で空間全体を覆う点群yiの構築は結構大変そう．）

　
　　
　　
　　k-means clusteringが，クラス多数を入力として必要とするのに対し．
　　Mean Shift Clusteringは，クラス多数の情報なしに，点群の粗密を解析しクラスタ分割を行える．
　　
　　

Mean Shift Image Filtering
　　Mean Shift Proceduerを利用すると，エッジを保存する画像の平滑化が行える．
　　

　　1. カラー画像 I , 画素位置に関するバンド幅h_s，画素値に関するバンド幅h_r を入力とする．

　　2. 画素 x_iは，その位置　(x_i,y_i) と　画素値 (L_i, u_i, v_i) を結合した，
　　　　画素位置-画素値-結合空間 (Bilateral Domain)内の点p_i (x_i,y_i, L_i, u_i, v_i)　であると考える．
　　　　全ての画素　x_i　について, そのBilateral Domain内の点p_iを計算しておく (5次元ベクトルにしておく)

　　3. 全てのp_i　にMean Shift Proceduerを計算し，収束位置をp_i^c = (x_i^c,y_i^c, L_i^c, u_i^c, v_i^c)とする．

　　4. x_iの画素値を, (L_i^c, u_i^c, v_i^c) で置き換える．

　　○Mean Shift Proceduerは次の通り計算する○
　　x^s, x^rをそれぞれ、5次元ベクトルの位置(2D)・色(3D)空間に対応するものとし，カーネル密度推定を以下の通り定義する．
　　　 $\displaystyle f(\bf{x}) = \frac{C}{N h_s^2 h_r^3}\sum_{i=1}^{N} k\left( ||\frac{\bf{x}^s-\bf{x}^s_i}{h^s}||^2 \right) k\left( ||\frac{\bf{x}^r-\bf{x}^r_i}{h^r}||^2 \right)$
　　Mean Shiftにより、次の通り位置を更新する. (勾配の求め方は前述の通り)
　　　
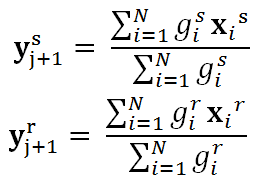
　　ただし
　　
　　

　　
　　
　　Mean Shift Image Filteringの結果 k(t) = 1-|t|を利用

　　　　
　　Original 　　　　　　　　　　　　　　　　　　　　　　　　h^s = 8,　 h^r = 8
　　　
　　　　
　　h^s = 32,　 h^r = 8　　　　　　　　　　　　　　　　　h^s = 32,　 h^r = 32

Copyright 2010~ Takashi Ijiri(井尻敬), All rights reserved.