Graph Cut Image Segmentation

概要: 非常に有名な画像領域分割手法．代表的な2通りの使い方がある．

　1)バイナリラべリング(前景/背景ラべリング). ユーザ(または自動アルゴリズム)が，前景領域内部と背景領域に複数のSeedを指定すると，「指定された前景/背景Seedに似た色を持つ画素が前景/背景になるよう」，「隣接画素の色の差が大きい部分にラベル境界が来るよう」，最適なラべリングが計算される．

　2) 複数領域ラべリング. 抽出したい領域の複数の代表画素を，ラベル毎に指定しておくと，「あるラベルの代表画素値と似た色の画素はそのラベルに属すよう」「隣接画素の色の差が大きい部分にラベル境界が来るよう」各画素をラべリングする．

　この手法の最大の特徴は，上記の要求を満たすエネルギー関数をうまく定義し，その最小化解が最大フロー(最小カット)問題を解くことで得られる事を利用して，高速に最適解(ラべリング)を計算する点である．Boykov先生らのグループがこの分野の先駆けで，基礎理論から応用まで幅広く発表している[1,2]．ここでは，ざっとGraph cut画像領域分割の基礎をまとめておく．

画像のバイナリラべリング

　前景領域の代表画素群P_fと背景領域の代表画素群P_bが与えられた下で，全ての画素x_i∊Pに前景ラベルFか背景ラベルBのどちらか一つを対応付けるバイナリラべリングを考える．前述した要求を満たすため，ラべリングは，なめらかで，かつ，画素値とconsistent(一貫している)である必要がある．なめらかさと一貫性に関する項を持った，以下のようなエネルギー関数が用いられる．

　　　　　　...(1)

ここでは，なめらかなラべリングとは，ラべリング結果の領域境界があまり入り組んでないという意味である．画像とラべリングがConsistentである(一貫している)とは，「似た色の画素どうしは同じラベルに属する」「あるラベルの代表色に似た色を持つ画素はそのラベルに属する」という意味である．まず，E_dataは，各画素x_iにラベルF or Bどちらをつけるのが不適当かを測る項で，以下のように定義する．

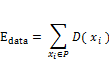
D(x_i)は，x_iにラベルF かBをつけるのがどの程度不適当かを測る関数で以下の通り定義する[3].

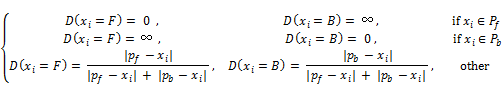
　エネルギー関数なので，付加するラベルが適当だと小さく，不適当だと大きな値になる事に注意．例えば一行目は，x_iが前景領域の代表画素である場合に，x_iにラベルBをつけるのは不適当であるためエネルギーが無限大になる．また，三行目の|p_f- x_i|は画素間の色の差を表す．複数の代表画素を指定する場合は注意が必要で，[3]ではx_iに一番近い色を持つx_f∊P_fとx_b∊P_b用いて，色の差を計算している．

E_smoothは，ラべリングのなめらかさを制御する項で，以下のようなエネルギー関数が良く用いられる．

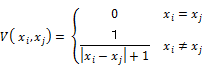
これは，隣接する2画素に異なるラベルが付けられた場合に，隣接画素の色の差に反比例するエラーを足すという意味になる．つまり，色差が大きい画素間に異なるラベルが付加されても大きなペナルティにはならないが，似た色を持つ隣接画素間に異なるラベルが付加されると大きなペナルティになる（discontinuity-preservingなどと呼ばれる性質）．

Graph Cutによるエネルギー最小化

ここで，重み付き無効グラフG={E,N}を次のように定義する．

-ノードN: 全ての画素x_iと前景ノードF背景ノードB (下図a)

-エッジE: 次のn-linkとt-lingの集合

--- n-link : 隣接画素間をつなぎ，重みV(x_i, x_j)を持つエッジ(下図b)

--- t-link :ノードF/Bと全ての画素間をつなぎ，重みD(x_i=F) / D(x_i=B)を持つエッジ (下図c)

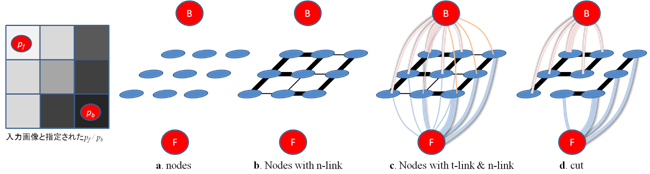
このグラフを，前景ノードFと背景ノードBをそれぞれ含む2個の部分グラフに分割する最小カットが，前述したエネルギー(1)の最小解となる．最小カットは，多項式時間でとける事が知られている．とりわけ上図のような構造のグラフであれば，実用的にはほぼ線形な計算時間で解く事が出来る．下図は2次元画像，3次元画像に関する実装結果．

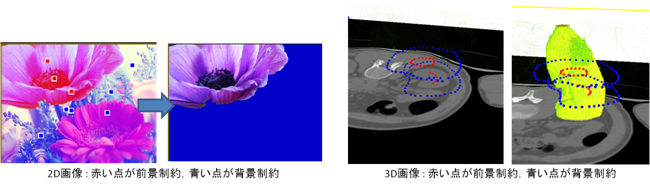
複数領域ラべリング

　ラベルがF/Bの2通りの場合は，前述の通り，ほぼ線形時間で計算できる．しかし，複数ラベル(領域)を扱おうとすると，複数の部分グラフに分ける最小カットを求める必要があり，その問題はNP困難になる [1]．そこで，[1]の論文では，NP困難な問題をそのまま解くのでなく，バイナリラべリングを繰り返す事で，近似解を得る2通りの方法を提案している．以下では，付加するラベルの集合を ℒとし，ラベルと画素の対応(ラべリング)をfと書く，f(x_i) ∊ ℒ．

α-β swap法．あるラべリングfを異なるラべリングf'へ変更する時，次の条件を満たす物をα-β swapと呼ぶ．

　　　α-β swap : 任意のラベルγ ≠ α, β (α, β, γ∊ℒ)についてf(x_i)=γ ならば f(x_i) = f'(x_i)

これはつまり，α，β以外の領域は変化しないラべリングの変更という意味であり，このα-β swapを用いて，以下のようなアルゴリズムが提案されている．

Algorithm A.

A-1) 任意の初期ラべリングfから開始

A-2) 全てのα, β ∊ ℒ のペアに対し以下を繰り返す．

A-2-1)エネルギーEを最小化するf'をα-β swapの範囲で計算する．

A-2-1)E(f' ) < E(f)であれば f=f'とする

A-3) A-2で一度でもfに変更があれば，A-2に戻る．

A2-1)では，元のラべリングfのα-βの領域のみに対し，バイナリラべリングを行えば良い事になる．つまり，α，βの領域のみから重み付きグラフを作成し，最小カットを計算すればよい．また，A2-2)のE(f)を計算する際には，グラフの最小カットの値でなく，全体のラべリングfを考慮したenergy E(f)の計算が必要なので注意する．論文[1]では，α-β swapの範囲で最小カットを計算しつつ，画像全体を考慮したエネルギーE(f)を求める手法が紹介されている．

α-expansion法: あるラべリングfを異なるラべリングf'へ変更する時，次の条件を満たす物をα-expansionと呼ぶ．

　　　α-expansion: α ∊ ℒ, X_α⊂ X'_α かつ，任意のl∊ℒについて X'_l⊂ X_l

ただし，X_l , X'_l は，ラべリングf, f'によるラベルlを持つ画素集合である，(X_l= {x_i| f(x_i) = l}, X'_l= {x_i| f'(x_i) = l}．この意味は，ラベルαを持つ領域のみが膨張し，他の領域を侵食する様なラべリングの変更である．これを用いて次のアルゴリズムが得られる．

Algorithm B

B-1) 任意のラべリングfから開始

B-2) 全てのα ∊ ℒ について以下を繰り返す．

B-2-1) エネルギーEを最小化するf'をα-expansionの範囲で計算する．

B-2-2) E(f' ) < E(f)であれば f=f'とする

B-3) B-2で一度でもfに変更があれば，B-2に戻る．

B-2-1では，元ラべリングfにおけるα領域とそれ以外領域とのバイナリラべリングをα-expansionの範囲で行う．これは単純にα領域のt-linkの値をD(xi=)=∞と置けばよい．得られた結果から，α，領域の更新を行う．計算前に領域で，かつ計算後も領域の画素は元のラベルを保持するようにする. B-2-2でE(f)を計算する際には，画像全体を考慮する必要がある．

Max flow / Min cut algorithm

実際に重み付きグラフの最大フロー最小カット問題を解くアルゴリズムについては，Boykov先生のページ参照．高速なアルゴリズムが，ソースごと公開されているので非常に便利．

[1]Yuri Boykov, Olga Veksler, Ramin Zabih, Fast Approximate Energy Minimization via Graph Cuts, PAMI, 1999.

[2]Yuri Boykov, Marie-Pierre Jolly, Interactive Organ Segmentation Using Graph Cuts, MICCAI, 2000.

[3]LI, Y., SUN, J., TANG, C. K., SHUM, H. Y.: Lazys-napping. In Proc. of ACM SIGGRAPH '04, 303–308, 2004.

井尻敬 @ 生物情報基盤, 理研

2011/11/15