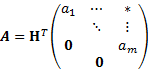ハウスホルダー(Householder)変換を用いたQR 分解(factorization)
概要:QR分解とは，行列A （n×m, n > m, rank(A) = m）を直交行列Q(n×n)と上三角行列R(n×m)の積に分解する手法である．連立方程式を解くときなどに活躍する．ここでは，グラムシュミットの直交化を用いたQR分解とHouseholder変換を用いたQR分解のアルゴリズムをまとめる
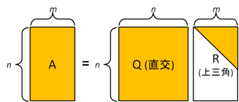
図1. QR分解
グラムシュミットの直交化を用いたQR分解
n×m行列A (n > m)，rank(A) = mは，n×n直交行列Qとn×m上三角行列Rの積，A=QRと分解できる（図1）．
Aのi列を列ベクトルaiで表す, A=( a1 a2 … am)．rank(A) = mなので，グラムシュミットの直交化により，m本の直交ベクトルbiが取得できる．
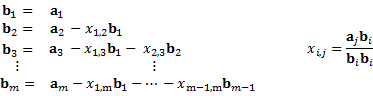
上式を次のように整理すると，
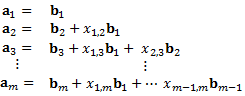
次の関係は明らかである．
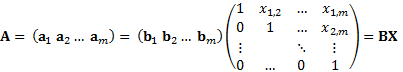
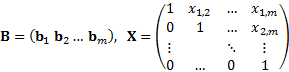
ここでBを直交化したいので，BXの間に，対角行列D=diag(||b1||, ||b2||, …, ||bm||), D-1=diag(1/||b1||, 1/||b2||, …, 1/||bm||),を挟む
n×m行列Q = (b1/||b1||, b2/||b2||, … , bm/||bm||)の列ベクトルは，n次元空間のm本の正規直行規定をなし，Rは上三角行列である(図2左)．Qを直交行列にしたいので，bi/||bi||に直交する(n – m)本の単位ベクトルを適当に選び，これを並べた各列に並べた行列をQ1とする．すると，
となり目的のQR分解を得られる．(Q Q1)はn×n直交行列である(図2右)．
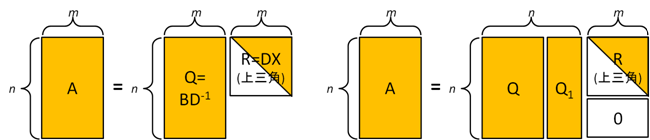
図2, QR分解
グラムシュミットの直交化法を用いるとQR分解が計算できる．しかし，グラムシュミットの直交化法は，逐次的に，既存のベクトルに直交する成分を引き延ばして利用する（正規化する）ため，計算機を用いて計算する場合には，数値的に不安定になる．これから説明するHouseholder変換を用いた方が安定といわれている．
Householder 変換を用いたQR分解
Householder変換とは，長さ等しい2本のn次元ベクトルx, yが与えられた時(||x||=||y||)，次のn×n行列Hで定義される線形変換のことである．
Inはn×n単位行列である．この変換は， xをyに，yをに移す変換である．
よってHx=yであり, Hy=xも同様に示せる．上の変形において xTx= yTy,yTx= xTyを用いた．また，Householder変換行列は，直交行列である．
Householder変換を用いたQR分解. 上記のHouseholder変換を用いて，QR分解を行う方法を考える．n×m行列A(n>m)が与えられ，k-1個のn×n直交行列H1, H2,…,Hk-1により既にk-1列目まで上三角行列に分解されているとする;
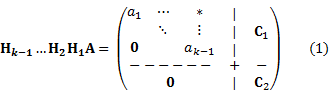
ここで「上式に左乗すると，k-1列目までの上三角性を失わず，k列目のk+1~n成分までをゼロにする．」という性質を満たすHouseholder変換Hkを求める．
天下り的だが，u =( 0 uk ), 0∊Rk-1, uk ∊Rn-k+1 というベクトルuが作るHouseholder行列は，
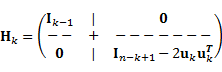
となり，これを式(1)の左辺に左乗する．
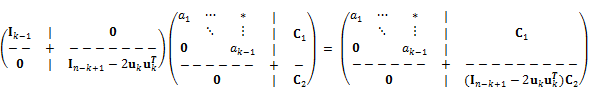
上式より，k-1列目までの上三角性は失われない事が分かる．さらに，k列目のk+1~n行の要素をゼロにしたい．つまり以下を満たす，ukを取得したい．
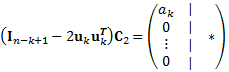
上式の
は，n-k+1次元のHouseholder変換であるので，ukを以下のように定義すればよい．
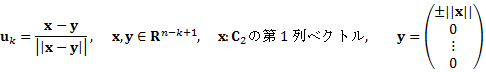
上の±はどちらの符号を選んでも良いが，xの第１成分と逆の符号を選んだ方が，桁落ちが少ない(u=x-yなので，同符号だと引き算による桁落ちの可能性がある)．
このukにより定義されるhouseholder変換
を式(1)の両辺に左乗すると
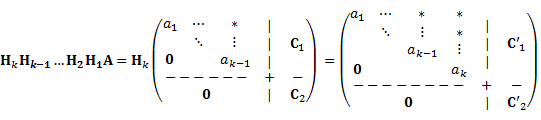
とk列目まで対角化できる．これを，m回繰り返すと，
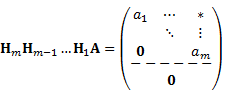
と上三角化できる．Householder変換の積 
は直交行列なので，H-1=HTを両辺に左乗すると
とQR分解が得られる(Q=HT)．
Householder変換によるQR分解アルゴリズム
+A-1)n×m行列A, n>m, rank(A)=mが入力される．
+A-2)準備
n×m行列Rを用意し R←A
n×n行列Qを用意し Q←In (用途によっては必要ない)
+ A-3)以下をm回繰り返す
+ A-3-1) k番目のHouseholder変換を次のように求める．
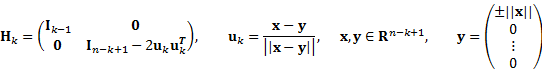
+ A-3-2) R←
R (HmHm-1…H1Aを求めている)
+ A-3-3) Q←Q (H=Hm Hm-1…H1を求めている.用途によっては必要ない)
+ A-4) A = QTRが得られる
高速化のための注意.
1) 上記アルゴリズムにおいて，Qは計算する必要のない事が多い(例えばAx=bの線形システムを解くときなどはQ= Hm Hm-1…H1の代わりにHm Hm-1…H1bを求めればよい．)．
2) u uTH (u∊Rn, H∊Rn×n)という積の計算が必要になるが，これを(u uT) Hと行列どうしの積にするとO(n3)かかるので， u (uTH)と計算する必要がある．後者だとO(n2)になる．
参考文献
[1] D.A.ハーヴィル (著), 伊理 正夫 (監訳), 統計のための行列代数 上.
井尻敬 @ 生物情報基盤, 理研
勉強した日 2012/4/12