GeoCut による画像領域抽出

概要: Boykov先生ら研究[1]．与えられた前景画素と背景画素制約を満たすように，前景領域を抽出する手法．前景と背景の境界曲線(3Dなら曲面)の長さ(3Dなら面積)が最小になるようなラべリングを計算する．Graph Cut領域分割の拡張で，隣接画素間のみでなく，n近傍にエッジを張る事により，境界曲線のL2 normの最小化が可能となった．境界曲線がImage manifold上のGeodesics(測値線)となるような，前景領域の計算も可能．Graph Cutの枠組みで，Active contourを解く手法とも考えられる．

　　実装自体は，Graph Cut領域分割の拡張で簡単にできる．また，エネルギーの定式化に積分幾何学の概念を用いており，説明がとても面白い．

参考文献 :

[1]Yuri Boykov, Vladmir Kolmogorov, Computing Geodesics and Minimal Surface via Graph Cuts, ICCV 2003.

実装方法

　導出は時間があるときにまとめるとして，実装方法に関して説明する．ただ実装するだけであれば，非常に単純なGraph Cut法の拡張でよい．入力として，画像と，前景領域の制約画素の集合pfと背景領域の制約画素の集合pbが与えられたとする．Graph Cut法では，以下のエネルギーを最適化した．

　　　　　　... (1)

E_data (t-link). E_dataは各画素xiに前景ラベルFと背景ラベルBのどちらをつけるのが不適当かを測る項であった．今回は，制約に関する画素のみに次のようなエネルギー関数を配置する．

　　　　

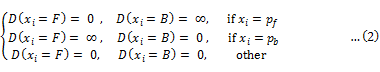
E_smooth (n-link): Geo cut法で重要なのは，E_smoothの項である．まず，簡単のため，単色の一様画像の場合を考える(真白の画像とか)．つまり，指定された前景/背景制約を満たしつつ，領域境界の曲線の弧長がなるべく短くなるラべリングを計算する事になる．Geo Cutでは，下図のように，同一方向のエッジがないような, 4近傍, 8近傍, 16近傍を繋ぐエッジを考える．エッジを反時計回り順にekと呼ぶ．

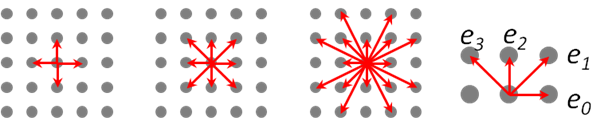
この近傍サイズが大きいほど，精度が上がる事になる．各エッジに次の重みを置く．
　　　　
はエッジの長さ，は画素のピッチ，次のエッジとの角度の差である．この重みの導出に積分幾何学を利用している[1]．以上で，Geo Cut法の実装に重要な要素は全て揃った．後は，Graph Cut法と同様に，式(2)から求まるt-linkと式(3)から求まるn-linkにより構成される，グラフの最小カットを求めればよい．

Image manifold上でのL2 normの最小化

式(3)のn-linkは，画像の色を考慮しないものだった．Geo Cut法では，与えられた画像 I(x,y)について，z = I(x,y)という曲面(Image manifold)を考え，この曲面上での境界曲線の長さを最小化する事により，境界曲線が画像のエッジに沿うようなラべリングを取得する．
　今，入力画像I(x,y)について，z = I(x,y)という曲面を考えると，(x,y)におけるリーマン計量Dは，次式である(この下に説明あり)．

　　　　

論文[1]では，このリーマン計量に変更を加た以下の物を用いている

　　　　

ただし，g(x)=exp(x2)．この曲面上での境界曲線の弧長を求めるには，n-linkの重み(式(3))を次のように変形すればよい．

　　　　

式(2)と式(5)を用いたグラフの最小カットを求めることで， Image manifold上での境界曲線の弧長を最小化するラべリングがが計算できる．

Image manifoldのリーマン計量

x-y平面上の曲線C:(x(t), y(t))がパラメータtにより定義されているとする．この時，点P0(t=0)からP1(t=s0)間の曲線の弧長は，

　　　　

となる．ここで，画像Iを，z = I(x, y)という曲面と考え，この曲面上の曲線C: r(t)=( x(t), y(t), I(x(t), y(t)) )における，点P0(t=0)- P1(t=s0)間の曲線の弧長は，第一基本形式を用いて次のように書ける．

この式(6)を，三次元曲線r(t)の距離ではなく，EFGが定義された２次元空間(x, y)内での距離と考える事もできる．この2次元空間は，空間がEFGにより歪んでいる．Euclid空間では，x方向にdx, y方向にdyだけ動くと全体の移動距離はds^2=(dx^2+dy^2)である．ところが，この歪んだ空間では，移動距離はds^2=(E dx^2+2F dx dy + G dy^2)になる．このds2の事をリーマン計量と呼ぶ．r(t)=( x(t), y(t), I(x(t), y(t)) )のリーマン計量は，

　　　　

となる．rx(t)=(1, 0, Ix), ry(t)=(0, 1, Iy)を利用した．これを踏まえて，論文[1]では，非一様なリーマン計量を以下のように定義している:

　　　　

ただし，g(x) = exp(-x2)．上式では，画素の微分値が小さい場所ほど，g(|▿I|)が大きくなり，Euclid距離に近づく．また，画素の微分値が大きい場所は，g(|▿I|)が小さくなる．この様な場所では，勾配方向に沿っている曲線は長く，勾配方向に垂直な方向では，長さが0に近くなる．(ds^2をリーマン計量と呼ぶと教科書にあったが，論文[1]中では，ds^2=(dx dy)D(dx dy)^TのDの事をRiemannian metricと呼んでいる．)

井尻敬 @ 生物情報基盤, 理研

2011/11/28